Who Invented Calculus?

Calculus is a superpower in math. From predicting planetary orbits to optimizing internet speeds, it’s been a cornerstone of countless advancements. But who invented this power tool? Actually, it took the collective genius of many mathematicians over millennia to develop the calculus we know today.

Ancient Calculus

Eudoxus and the Method of Exhaustion

Imagine trying to figure out the area of a circle by filling it with shapes that approximate it. If you use a triangle there are some big gaps, but if you use a square, then a regular hexagon, then a regular octagon, those gaps start to shrink and the areas of the two shapes get closer. Eudoxus used this technique, known as the method of exhaustion, to find the areas of circles, solids, and spheres, and this is the first known example of the idea of a limit.

Archimedes and Tangents

Fast forward 100 years, and we meet Archimedes. He built upon Eudoxus’s work and began exploring methods to calculate the tangent line to shapes other than the circle. Using polar coordinates he was able to calculate the slope of a line tangent to an Archimedes’ spiral given by the polar equation $r = a\theta$, where a is a constant. Archimedes was the first mathematician to do so. Nowadays, these computations would be done using derivatives, but because they had not yet been invented, Archimedes had to use more primitive tools, viewing the spiral as a series of line segments and seeing what happened as the line segments got shorter, essentially using a limit. Archimedes was a trailblazer, paving the way for future developments.

Other Calculus Discoveries Throughout the World

Between the Ancient Greeks and the Renaissance in Europe, developments in calculus were slow. The mathematicians in the Middle East, the math powerhouse at the time, mainly focused on algebra and geometry, making huge developments in those fields, but did not concern themselves with calculus. The next big name in calculus was Nicole Oresme, a French philosopher who contributed to economics, physics, astronomy, theology, and mathematics.

Around the mid-3rd century AD, in the other part of the world, the Chinese mathematician Liu Hui came up with his own version of the “method of exhaustion,” independently of Eudoxus. Other developments came later from the Middle East and India, in the 11th and 14th centuries, respectively, but the study of calculus was a slow march that did not capture the world’s attention. In the 14th century, all of that changed.

Calculus in the Medieval Times

Nicole Oresme

Born in 1325, Oresme was one of the only significant European mathematicians for centuries. The inventor of the “+” sign, he was the first to graph quantities, foreshadowing Descartes’ coordinate plane, and showed that the Harmonic Series \(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dots\) diverges in the following way:

\[ \dfrac{1}{2} = \dfrac{1}{2} \]

\[ \dfrac{1}{3} + \dfrac{1}{4} > \dfrac{1}{4} \cdot 2 = \dfrac{1}{2} \]

\[ \dfrac{1}{5} + \dfrac{1}{6} + \dfrac{1}{7} + \dfrac{1}{8} > \dfrac{1}{8} \cdot 4 = \dfrac{1}{2} \]

 

And so on, grouping fractions in sets of 1, 2, 4, 8, and so on to prove that \(\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \dots > \dfrac{1}{2} + \dfrac{1}{2} + \dfrac{1}{2} + \dots = +\infty\).

Additionally, he stated a version of the fundamental theorem of calculus, stating that the area underneath a velocity-time graph was equal to the distance traveled. Because velocity is the time derivative of position, he was essentially saying that

\[ \int_a^b f'(t)\, dt = f(b) – f(a) \]

However, he did not generalize this to any function, so he is not credited with the discovery of the FTC. Still, he was extremely important to the eventual discovery of calculus.

Madhava of Sangamagrama

Madhava was an Indian mathematician who lived in the 14th and early 15th centuries (the exact dates are unknown). He pioneered trigonometry and infinite series long before they were independently discovered in Europe. While there is no evidence his ideas were transmitted to Europe (and thus the creators of calculus as we know it), he is still worth mentioning.

Madhava studied infinite series, including the power series for the inverse tangent, which he wrote as

\[\theta = \tan\theta – \dfrac{\tan^{3}\theta}{3} + \dfrac{\tan^{5}\theta}{5} – \dfrac{\tan^{7}\theta}{7} + \cdots\]

On this note, he made contributions to trigonometry and constructed sine and cosine tables accurate to 7 decimal places! He also approximated \(\pi\) to 12 decimal places by using the infinite series.

Calculus Takes Shape

Pierre de Fermat

Pierre de Fermat (1607-1665) is one of the best-known mathematicians ever due to his Last Theorem, Little Theorem, and Fermat primes, as well as making fundamental discoveries in probability, optics, and analytic geometry, a precursor to calculus. Fermat discovered a method of finding tangents to curves.

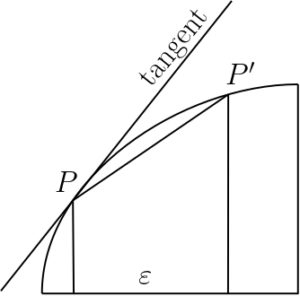
This method involves drawing a line between a point \(P\) and another point \(P’\) on the curve, and then letting \(P’\) get closer and closer to \(P\), so that \(\varepsilon\) gets closer and closer to \(0\) and the line \(\overline{\text{PP’}}\) approximates the tangent line \(PT\) better and better. The formula to find the slope of the tangent line can then be given by \(m = \displaystyle \lim_{\varepsilon\to0} \dfrac{f(x + \varepsilon) – f(x)}{\varepsilon}\), which you may recognize as the formula for a derivative. Fermat also noticed that the sum under a curve given by \(f(x) = x^n\) was equal to \(nx^{n-1}\), which is equivalent to the power rule for integration. However, it is not known whether he figured out that derivation and integration were inverses of each other, which is one reason why he is not credited with the invention of FTC just like Oresme.

Kepler’s Integral Calculus

In 1615, German mathematician Johannes Kepler published a groundbreaking work that laid the foundation for integral calculus. His interest was sparked when a merchant who was selling him wine used an inconsistent method to calculate how much wine was in each barrel. Kepler thought that there must have been a better way and so he set out to study volumes and areas. Through his studies, he derived a rule that served as an approximation of integrals similar to Riemann sums. Here is the rule he discovered for approximating definite integrals, also known as Simpson’s Rule:

\(\displaystyle\int_a^b f(x)\, dx \approx \frac{b-a}{6}\left[f(a)+4f\left(\frac{a+b}{2}\right)+f(b)\right]\)

Kepler was a major figure during the Scientific Revolution, which saw huge leaps in our understanding of the world. Apart from mathematics, his work in astronomy – especially his laws of planetary motion – inspired a young man named Isaac Newton.

Isaac Newton: Father of Modern Physics

Newton, famous for his work in physics and the story of the falling apple, is one of the key figures in the development of calculus. Newton was not limited in his studies and made great developments in calculus and physics as the two disciplines were inextricably linked. As the story goes, Newton sat under a tree one day taking a nap, and was hit in the head by an apple. Where most people would walk away with nothing more than a bump on their head, Newton walked away with the beginnings of a major scientific realization: all objects obey the rule of universal gravitation. While this story is more based in folklore than reality and it is likely that he merely witnessed an apple falling, his breakthrough itself is historically factual. Following this incident, Newton developed the core principles of Newtonian Mechanics. In 1948 the unit of force called the “Newton” was officially adopted in his honor. However, Newton was faced with a big obstacle – the mathematics necessary to describe the science of motion had not yet been developed. Newton found an elegant solution to this problem – he developed the mathematics himself! He called his theory “fluxional calculus,” which was very effective in describing motion. During the 1660s and 1670s, Newton made significant advancements, but he wasn’t alone in his discoveries.

Isaac Newton, famous for revolutionizing physics and calculus, is generally credited for inventing calculus, along with Gottfried Leibniz. While the story about an apple falling on Newton’s head is likely apocryphal, it is likely that a falling apple did inspire his law of universal gravitation, building on Galileo’s earlier work. Upon delving deeper into physics, he wanted a way to describe the motion of large objects, such as planetary motion; one of his biggest breakthroughs was using calculus to prove that the orbits of the planets were ellipses, which agreed perfectly with Tycho Brahe’s measurements of planetary motion from the Uraniborg observatory. Newton mainly saw calculus as a way to describe motion, and the notation for his “fluxional calculus” could differentiate or integrate with respect to time. He was most productive during the 1660s and 1670s but did not publish his work until 1687, leading to one of the greatest mathematical feuds of all time.

Newton vs. Leibniz

Two Minds, One Discovery

Have you ever thought you had a brilliant idea, only to find out someone else had it too? That’s exactly what happened with Newton and his German contemporary, Gottfried Leibniz. Both discovered key aspects of calculus around the same time.

Newton focused on differential calculus, coming up with the concept of derivative as a way to describe change, although he was, with his. His big breakthroughs happened during the 1665-66 London plague when he was isolated on a farm, where the story of the falling apple allegedly took place. Some researchers have called this his annus mirabilis, or miraculous year, in which he uncovered laws of gravity, optics, motion, and calculus. 

Leibniz’s breakthroughs came several years later as the young German mathematician was convinced to study calculus by Dutch Mathematician Christiaan Huygens in 1672. Leibniz embarked on a fierce exploration of calculus in the following years, and soon he began to make headway. He reasoned that the slope of a line was a ratio of the change in the “ordinate” (y-coordinate) to the change in the “abscissa” (x-coordinate). He then reasoned that an integral was the sum of infinitely small ordinates across one abscissa or a sum of all of the infinitely thin rectangles beneath a curve. This was one of Leibnitz’s biggest breakthroughs, as he realized that the slope of a tangent and integral were inverse operations, which is the fundamental theorem of calculus. He knew his discoveries were special and took pains to create a notation to convey them.

Between October and November of 1675, Leibniz formalized his notation creating much of the common calculus we use today such as the large s-shaped integral sign and using ‘dx’ and ‘dy’ to describe the infinitely small ordinates and abscissas:

$$\displaystyle\int_a^bf(x)dx \qquad\frac{dy}{dx}$$

Both Leibniz and Newton made great contributions to the calculus we use today, but, although Newton discovered calculus first, Leibniz published his work first, leading to a huge dispute between them.

Controversy

As people recognized the profound significance of the discoveries made by Newton and Leibniz, one question persisted: who discovered calculus first? Initially, this question did not seem to matter. Both Newton and Leibniz had independently discovered the fundamental principles of calculus, and they appeared to respect each other’s achievements. Although they had some disagreements over the details and methods of calculus, they did not question each other’s integrity. 

All that changed in 1695 when a British mathematician, John Wallis, started a fire he couldn’t put out: he accused Leibniz of plagiarizing Newton’s work! What ensued was a dirt-slinging insult battle with drama to rival a Shakespearean play.

Newton embarked on a smear campaign to silence Leibniz to make sure that he, and only he, would be remembered as the “father of calculus.” He spread rumors that Leibniz had some of his early calculus manuscripts and that he had written letters to Leibniz discussing these topics. When Leibniz’s friends tried to defend him, Newton turned up the heat and pressured them into taking back anything they said.

Soon the mathematical community lost its trust in Leibniz and hailed Newton as the true father of calculus. In 1713 the Royal Society, which Newton was the president of (talk about bias!), published an official paper proclaiming that Newton was the first in the calculus race and that Leibniz had been influenced by Newton.

Sadly, after taking punch after punch from Newton and his cronies, Leibniz died poor and dishonored without much to his name, but since then history has been kinder to him. Mathematicians eventually realized that Leibniz invented much more effective notation. It was widely adopted and it is now used worldwide. Here is Newton’s notation for derivatives and integrals with the dot notation referring to derivatives and the prime notation to integrals. Newton’s notation for integrals was inconsistent and unintuitive, which introduced significant difficulties:

\(\text{derivative: } \dot{y} \qquad \text{integral: } y’, \boxed{\phantom{y}} y, \boxed{y}\)

Source: https://en.wikipedia.org/wiki/Notation_for_differentiation#Newton’s_notation_for_integration

While Newton’s notation can be used and actually is used by physicists, Leibniz’s notation is more specific as it identifies both the variable of integration and differentiation and it emphasizes the ratio relationship between dy and dx. In addition to this, Newton’s notation for integrals would be confusing, since it’s exactly the same as Joseph-Louis Lagrange’s derivative notation – Lagrange used the prime symbol to denote derivatives, while Newton used it to denote antiderivatives. This is why mathematicians use Leibniz notation for derivatives and integrals.

Historians now believe that Newton and Leibniz independently discovered calculus without any foul play. Still, due to the contentious circumstances of the debate, England clung to Newton’s more cumbersome notation for over 100 years, ignoring many mathematical advancements occurring in mainland Europe. As a result, they fell significantly behind in mathematics and the physical sciences. Morris Kline aptly described this situation in his book Mathematical Thought from Ancient to Modern Times Volume Two, stating, “The English settled down to study Newton instead of nature” (Kline, pg. 622). Instead of using Newton’s and Leibniz’s work as a springboard for new discoveries in mathematics and physics, as most of Europe did, they effectively isolated themselves from global mathematical developments, leading to over a century of stagnation. During this period, they produced only a few notable mathematicians and failed to make significant advances in math or science. It wasn’t until the British adopted more modern notation in the 1820s that they began to catch up with their international peers. England’s Unwavering devotion to Newton indeed contributed to its decline in scientific progress.

Further Developments

After the time of Newton and Leibniz, calculus underwent profound developments that continued to enrich its theory and applications. Augustin-Louis Cauchy rigorously defined limits, continuity, and derivatives in the 19th century establishing a true foundation for calculus. Mathematicians like George Berkeley had expressed skepticism about infinitesimals and other shaky parts of calculus theory, but Cauchy’s work silenced him and other skeptics. Karl Weierstrauss continued Cauchy’s work formalizing the definition of a function. After the work of these two men, no one would successfully question the validity of the core tenets of calculus. 

New innovations kept pouring in as Leonard Euler extended calculus to include functions of complex numbers and introduced the notation we use today, while Lagrange developed the method of Lagrangian mechanics, similar to Newtonian Mechanics except more focused on energy than on forces. These developments and so many more enabled calculus to flourish as a rigorous mathematical discipline in modern science.

Conclusion

You now know a lot more about the development of calculus and the story of the controversy between Leibniz and Newton which led to mathematical stagnation in England. The moral of the story is that the key to succeeding in mathematics is using correct notation!

Sources

Facebook
Twitter
LinkedIn
WhatsApp
I Aced Calculus team

I Aced Calculus team

More articles