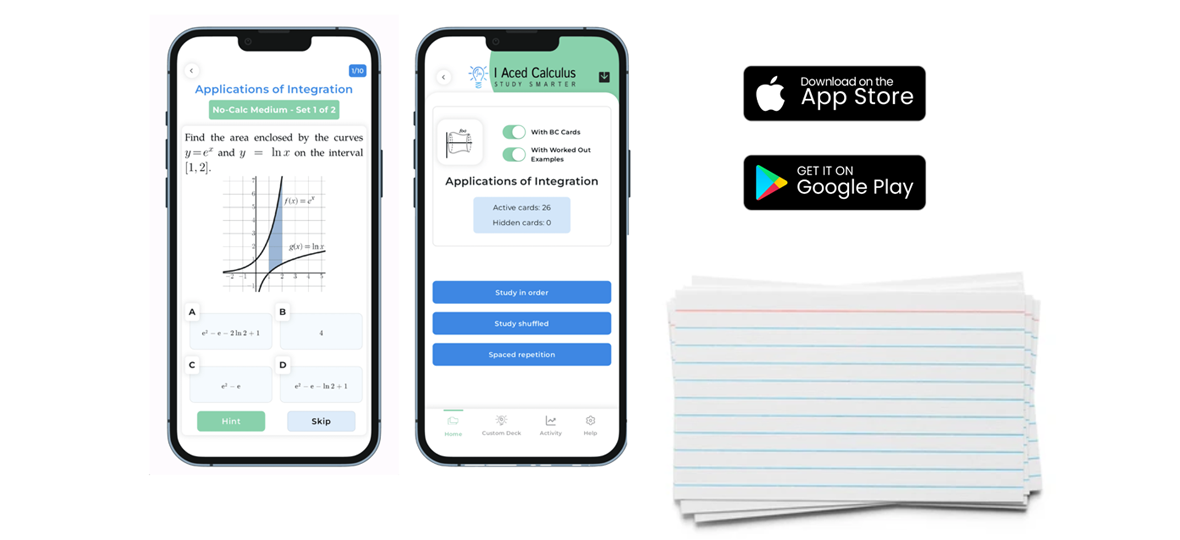
Spaced Repetition
1. Summary Spaced Repetition is a learning technique that shows flashcards that are difficult for you more frequently than easier ones. For instance, the I Aced Calculus (IAC) app asks users to rank how well they understood a flashcard on a scale from 1 to 5. Then, it employs an algorithm to decide what questions…
Read article