Introduction to Radian and Degree Conversion
Trigonometry often uses radians as a way to measure angles, although degrees are also common in many applications. Knowing how to convert between these units is essential. The main relationship between radians and degrees is:
\[\begin{align*} \pi \text{ radians} = 180^\circ \end{align*}\]
If we divide both sides by 3 we get
\[\begin{align*} \dfrac{\pi}{3} \text{ radians} = \dfrac{180^\circ}{3} = 60^\circ \end{align*}\]
So, \(\dfrac{\pi}{3}\) radians is equivalent to 60 degrees. However, the conversion might not be as straightforward. For example, this is how one would convert $\dfrac{7\pi}{5}$ radians to degrees:
\[\begin{align*} \dfrac{7\pi}{5} = \dfrac{7\pi}{5}\cdot\dfrac{180^\circ}{\pi} = 252^\circ \end{align*}\]
Finding \(\cos \dfrac{\pi}{3}\) Using a Triangle
To find
\[\begin{align*} \cos\dfrac{\pi}{3}=\cos 60^\circ \end{align*}\]
we use a 30-60-90 triangle:
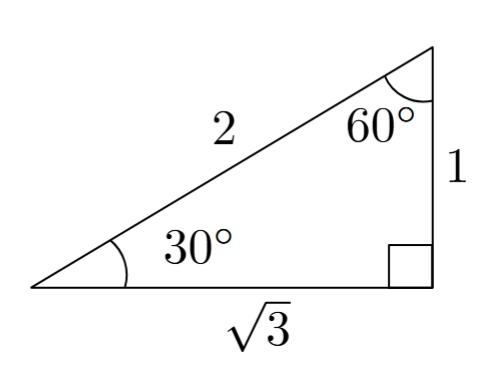
From the triangle, it is clear that
\[\begin{align*} \cos60^\circ = \boxed{\frac{1}{2}} \end{align*}\]
Finding \(\cos \dfrac{\pi}{3}\) Using the Unit Circle
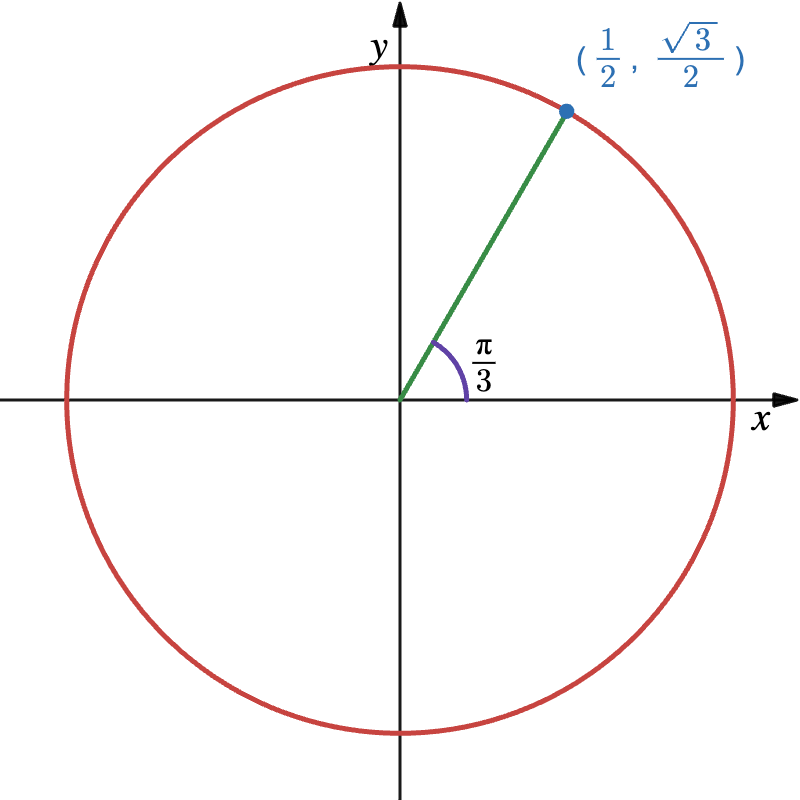
If you memorized the unit circle and remember that the \(x\)-coordinate of a point corresponds to the cosine of the angle, you can draw the diagram above and conclude that
\[\begin{align*} \boxed{\cos \dfrac{\pi}{3} = \dfrac{1}{2}} \end{align*}\]
Example Problem Involving \(\cos \dfrac{\pi}{3}\)
A ladder leans against a wall, forming a $60^\circ$ angle with the ground. If the ladder is 10 feet long. How far is the ladder’s base from the wall?
Solution
When possible, you should always draw a diagram to help you solve the problem. In our case, the diagram looks like this:
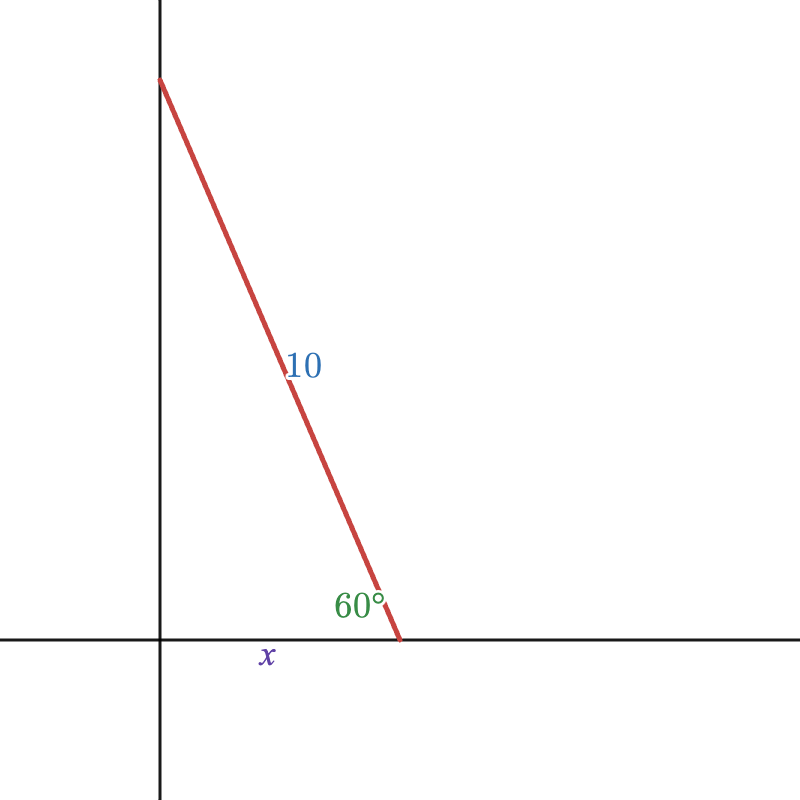
Let the distance from the base of the ladder to the wall be \(x\). Since the angle between the ladder and the ground is 60 degrees, we can use the cosine function:
\[\begin{align*} \cos 60^\circ = \dfrac{\text{adjacent}}{\text{hypotenuse}} = \dfrac{x}{10} \end{align*}\]
Substitute \(\cos 60^\circ = \dfrac{1}{2}\) and solve for \( x \):
\[\begin{align*} \dfrac{1}{2} = \dfrac{x}{10} \end{align*}\]
\[\begin{align*} x = 10 \cdot \dfrac{1}{2} = \boxed{5 \text{ feet}} \end{align*}\]
Thus, the base of the ladder is 5 feet from the wall.
