Unit Circle

The unit circle is defined by $x^2 + y^2 = 1$, which is a circle with radius $1$, centered at the origin $(0, 0)$. An example of the unit circle is below:

Standard Position of an Angle

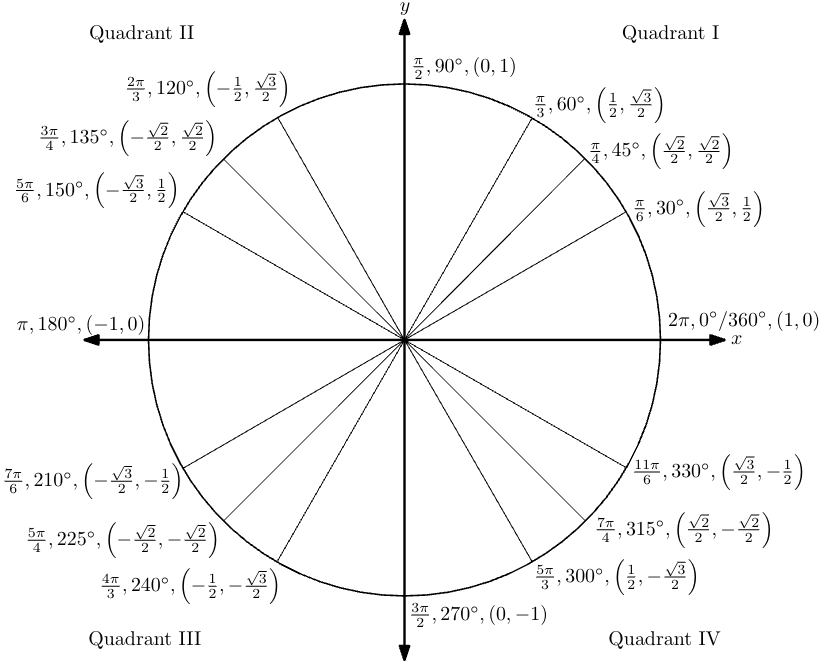
An angle is in standard position if its initial side is on the positive $x$-axis, its vertex is at the origin and it is measured counterclockwise from the initial side to the terminal side. The unit circle above gives the radian measure, the degree measure, and the point where its terminal side intersects the unit circle for some common angles. The point where the terminal side of angle $\theta$ intersects the unit circle is defined by $(\cos\theta, \sin\theta)$. In other words, $\cos \theta$ is the $x$-coordinate of the intersection point and and $\sin \theta$ is the $y$-coordinate.

Trig Values of an Angle

For example, looking at the $120^\circ$ angle, we see that the radian measure is $\dfrac{2\pi}{3}$. In addition, the $x$- and $y$-coordinates of the intersection, and we know that $\cos 120^\circ = -\dfrac12, \sin 120^\circ = \dfrac{\sqrt3}2$. This gives the point $\bigg(\!\!-\dfrac12, \dfrac{\sqrt3}2\bigg)$.

Using Special Right Triangles

While the values and angles in the unit circle look complicated, there are a lot of patterns and symmetry that can help you memorize the whole thing. If you look carefully, the first quadrant is duplicated in quadrants II, III and IV. You might also notice that the $x$- and $y$-coordinates for the corresponding points on the unit circle have the same values but different signs. In fact, it is sufficient to memorize the ratios in the 30-60-90 right triangle and the 45-45-90 right triangle to be able to figure out all values of special angles on the unit circle:

Reference Angle

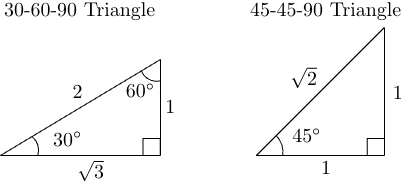
To leverage the symmetry in the unit circle, we define the reference angle as the angle between the terminal side and the $x$-axis. The measure of the reference angle is always between $0^\circ$ and $90^\circ$. For example, $180^\circ$ has a reference angle measuring $0^\circ$, $270^\circ$ has a reference angle of $90^\circ$ and $240^\circ$ angle has the reference angle measuring
$$240^\circ – 180^\circ = 60^\circ$$

Example: find $\sin 240^\circ$

1. Calculate the reference angle:
   $$240^\circ – 180^\circ = 60^\circ$$
2. Calculate the sine of the reference angle either from memory or by using a special triangle:
   $$\sin 60^\circ = \dfrac{\sqrt3}{2}$$
3. Assign the sign to the value based on the quadrant: Notice that $240^\circ$ lies in quadrant III and $\sin x$ corresponds to the $y$-coordinate of the point. Since the $y$-coordinate is negative in quadrant III, $\sin 240^\circ$ must also be negative. Hence, the answer is
   $$\boxed{-\dfrac{\sqrt3}{2}}$$.