Have you ever had trouble remembering when sines, cosines, and tangents are positive or negative? If so, you may want to remember the mnemonic ASTC, which stands for All, Sine, Tangent, Cosine and can be remembered as “All Students Take Calculus.” The acronym tells you which trig functions are positive in each quadrant, starting from quadrant I and going counterclockwise:
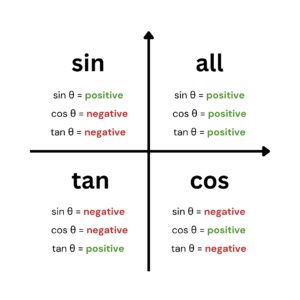
Here is the expansion of the mnemonic for each quadrant:
- All: All trigonometric functions are positive.
- Students: Sine is positive.
- Take: Tangent is positive.
- Calculus: Cosine is positive.
And that’s it! This mnemonic is easy to remember and understand, and it can be a lifesaver when it’s hard to remember what’s positive and what’s negative. Here are some examples of the many uses of ASTC:
Examples
Example 1: Finding Trigonometric Functions in Quadrants
Let’s apply the mnemonic to find the signs of trigonometric functions in different quadrants:
Question: What is the sign of $\sin(120°)$?
Answer: Using the ASTC mnemonic, only sine is positive in quadrant II. Therefore, $\sin(120°)$ is positive.
Question: What is the sign of $\tan(315°)$?
Answer: Using the ASTC mnemonic, only cosine is positive in quadrant IV, so $\tan(315°)$ is negative.
Example 2: Trigonometric Identities
Using the mnemonic to solve problems using trigonometric identities:
Given that $\sin(\theta) = \frac{3}{5}$ and $\theta$ is in Quadrant II, find $\cos(\theta)$ and $\tan(\theta)$.
Because $\sin^2(\theta) + \cos^2(theta) = 1$, the magnitude of \cos(\theta) must be $\frac{4}{5}$. But is $\cos(\theta)$ positive or negative? Looking at ASTC, we see that in Quadrant II only sine is positive, so $\cos(\theta) = \boxed{-\frac{4}{5}).$
Why it works
This mnemonic works because $\sin(x)$ is the $y$ coordinate of the unit circle, $\cos(x)$ is the $x$ coordinate of the unit circle, and $\tan(x) = \dfrac{\sin(x)}{\cos(x)}$. In Quadrant I, both the $x$ and y coordinates are positive, so all of $\sin(x)$, $\cos(x)$, and $\tan(x)$ are positive. In Quadrant II, the $y$ coordinate is positive and the $x$ coordinate is negative, so $\sin(x)$ is positive, and $\cos(x)$ and $\tan(x)$ are negative. In Quadrant III, both the x and y coordinates are negative, so $\sin(x)$ and $\cos(x)$ are negative and $\tan(x)$ is positive. In Quadrant IV, the $y$ coordinate is negative and the $x$ coordinate is positive, so $\cos(x)$ is positive while $\sin(x)$ and $tan(x)$ are negative.
Conclusion
The ASTC mnemonic is very useful for helping you remember the signs of trig functions, but it’s important not to lose sight of the reason why it works – sine is the $y$ coordinate, cosine is the $x$ coordinate of the point on the unit circle, and tangent is sine divided by cosine. Understanding this will deepen your grasp of trigonometric concepts, ensuring you not only remember ASTC but also understand how trig functions behave within the coordinate system.
