The value of \(\cos 180^\circ\) is:

$\cos 180^\circ = \boxed{-1}$

Explanation

To understand why, let’s look at the unit circle. The cosine of an angle corresponds to the \(x\)-coordinate of the point on the unit circle at that angle. We measure angles by moving counterclockwise from the positive \(x\)-axis. Thus at \(180^\circ\), we’re at the opposite side of the unit circle at the point with coordinates \((-1, 0)\).

Here, the \(x\)-coordinate is \(-1\), which is the value of \(\cos 180^\circ\).

Unit Circle Diagram

Why is it \(-1\)?

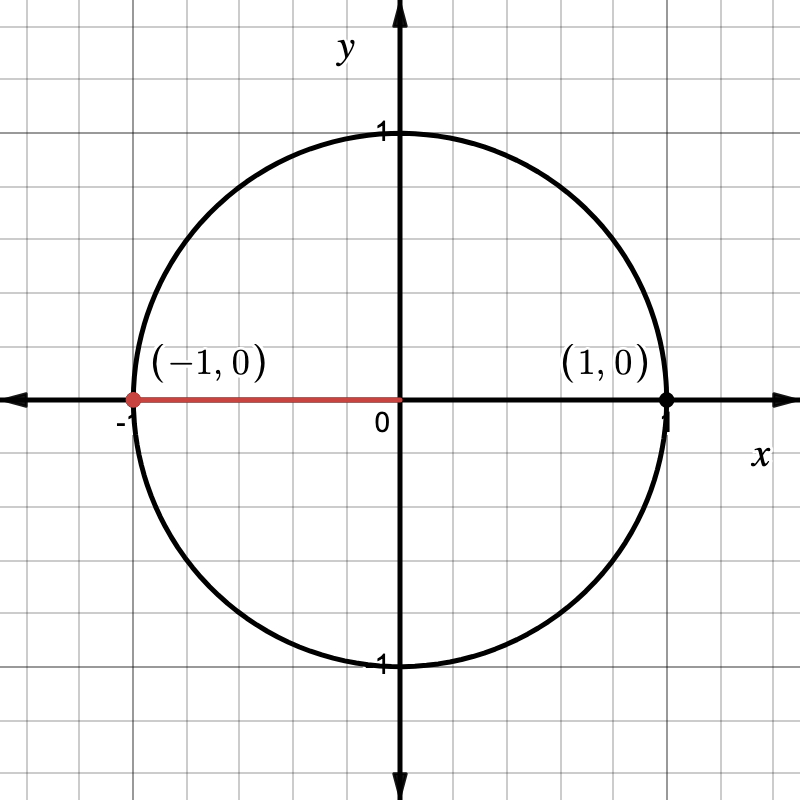
The unit circle helps visualize this because angles measured from \(0^\circ\) which is the direction of the positive \(x\)-axis (starting at \((1, 0)\) lead us along the circle to the \(180^\circ\), which is furthest point on the left side of the circle. The value of \(\cos\) of the given angle is the \(x\)-coordinate of the point on the unit circle. This is also why \(\cos\) of \(0^\circ\) is \(1\), and \(\cos\) of \(90^\circ\) is \(0\) – look at the \(x\)-coordinates of those points.

Therefore, \(\cos 180^\circ = \boxed{-1}\).