Introduction
Everyone knows \(\pi\). The ratio between the circumference and diameter of a circle is often approximated as 3.14. For many, it’s the first irrational number they encounter—a number so renowned that it even has its own day of celebration. But how was \(\pi\) actually discovered?
The history of \(\pi\) stretches over thousands of years, reflecting humanity’s deep fascination with the fundamental properties of circles. The earliest approximations of \(\pi\) are attributed to the Egyptians and Babylonians around 1900-1600 BCE. During the first millennium, Greeks and Chinese made significant progress in estimating \(\pi\) with increasing precision.
Early Approximations
Around 250 BCE, the Greek mathematician Archimedes used a polygonal approximation to estimate \(\pi\). He calculated that:
\[ \frac{223}{71} < \pi < \frac{22}{7} \]
which translates to approximately:
\[ 3.1408 < \pi < 3.1429 \]
The polygonal approximation involved calculating the perimeters of inscribed and circumscribed polygons, which provided lower and upper bounds for the perimeter of a circle. By continuously doubling the number of sides, Archimedes could refine the bounds and estimate \(\pi\).
Polygonal approximation
Centuries later, Greek mathematician Ptolemy was able to pinpoint the value of \(\pi\) to about 3.1416 in 150 AD using a similar method.
Similarly, Chinese mathematician Liu Hui used a polygon-based algorithm in 264 AD to accurately determine \(\pi\) to 5 digits. Zu Chongzhi later applied Liu’s algorithm to a 12,288-gon to determine 8 digits of \(\pi\), which held the record for the most accurate value of \(\pi\) until the 1300s. During this period, Indian mathematician Madhava of Sangamagrama discovered the Maclaurin series for \(\arctan(x)\) and was able to calculate 13 digits of \(\pi\) using it:
\[ \pi = 4\left(1 – \frac{1}{3} + \frac{1}{5} – \frac{1}{7} + \cdots\right) \]
Advancements in Series
During the next few centuries, few advancements were made in new formulas or methods of calculating \(\pi\). Most mathematicians who broke previous records during this time used polygons with increasingly large numbers of sides to approximate \(\pi\). In 1630, Austrian astronomer Christoph Grienberger obtained 39 digits of \(\pi\) using a 1040-sided polygon.
The search for more digits of \(\pi\) was revolutionized in the late 1600s with the use of infinite convergent series. In 1671 and 1673, Scottish mathematician James Gregory and German mathematician Gottfried Wilhelm Leibniz independently discovered the Taylor series for \(\arctan(x)\), known as the Gregory-Leibniz series:
\[ \arctan z = z – \frac{z^3}{3} + \frac{z^5}{5} – \frac{z^7}{7} + \cdots \]
By substituting \(z=1\), we get the formula known as the Leibniz formula for \(\pi\):
\[ \frac{\pi}{4} = \sum_{k=1}^\infty \frac{(-1)^{k+1}}{2k-1} = 1 – \frac{1}{3} + \frac{1}{5} – \cdots \]
However, this series converges too slowly to practically determine \(\pi\) past 39 digits. For example, after 100 terms, the sum is roughly 3.15149, and each digit requires roughly ten times as many terms to determine compared to the previous sum.
In 1699, English mathematician Abraham Sharp substituted \(z=\frac{1}{\sqrt{3}}\), which set the series to converge to \(\arctan(\frac{1}{\sqrt{3}}) = \frac{\pi}{6}\). This series converged much faster, allowing approximation of \(\pi\) up to 71 digits.
In 1706, John Machin, a British professor of astronomy, created the following series using the Gregory-Leibniz series:
\[ \frac{\pi}{4} = 4 \arctan \frac{1}{5} – \arctan \frac{1}{239} \]
This series converged much faster, allowing for approximation of \(\pi\) up to 100 digits. In 1844, Zacharias Dase set a new record using a similar Machin-like formula to reach 200 digits of \(\pi\):
\[ \frac{\pi}{4} = \arctan \frac{1}{2} + \arctan \frac{1}{5} + \arctan \frac{1}{8} \]
Notably, in 1910, Indian mathematician Srinivasa Ramanujan discovered multiple infinite series of \(\pi\) that converged rapidly. Ramanujan’s formulas have become the main method for determining \(\pi\) due to their accuracy and efficiency:
\[ \frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^\infty \frac{(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}} \]
Modern Computation
The quest for more digits of \(\pi\) was revolutionized in the 20th century with the advent of computers. In 1961, Daniel Shanks calculated \(\pi\) to 100,000 digits using a desk calculator. In 1989, the Chudnovsky brothers calculated 1 billion digits of \(\pi\) using the variation of Ramanujan’s series:
\[ \frac{1}{\pi} = 12 \sum_{k=0}^\infty \frac{(-1)^k (6k)! (13591409 + 54514013k)}{(3k)!(k!)^3 640320^{3k + \frac{3}{2}}} \]
All subsequent records have been set using the Chudnovsky algorithm. The most recent record of 202 trillion digits was achieved in June 2024 using a program called y-cruncher.
Calculating \(\pi\) with Calculus
Now let’s look at a simple way to compute \(\pi\) using elementary calculus! Those who have studied limits know that as \(x\) approaches 0, \(\frac{\sin(x)}{x}\) will approach 1.
\[ \lim_{x \to 0} \frac{\sin(x)}{x} = 1 \]
If we set \(x = \pi/n\) then we get this limit.
\[ \lim_{\frac{\pi}{n} \to 0} \frac{\sin \frac{\pi}{n}}{\frac{\pi}{n}} = 1 \]
We can simplify this limit by multiplying both sides by \(\pi\) and moving \(1/n\) in the denominator to the numerator. We then notice that \(\pi/n\) approaching 0 entails that \(n\) approaches infinity.
\[ \lim_{n \to \infty} n \cdot \sin \frac{\pi}{n} = \pi \]
We know that \(\sin(\pi/6) = \frac{1}{2}\) and \(\cos(\pi/6) = \frac{\sqrt{3}}{2}\). We also know the half-angle formulas for sine and cosine.
By using \(\sin(\pi/6) = \frac{1}{2}\) and \(\cos(\pi/6) = \frac{\sqrt{3}}{2}\) as well as the half-angle formulas, we can find values for \(\sin(\pi/12)\), \(\sin(\pi/24)\), \(\sin(\pi/48)\), \(\sin(\pi/96)\), and so on.
By plugging in these values into the limit shown above, we can find \(n \cdot \sin(\pi/n)\) as \(n\) approaches infinity, which, as we determined in the limit above, equals \(\pi\).
Thus, we can approximate \(\pi\) to greater degrees of certainty as \(n\) approaches infinity. This is a table of values up to \(n=384\). As shown in the table, the values of \(n \cdot \sin(\pi/n)\) become closer and closer to \(\pi\) as \(n\) approaches infinity. This is a relatively simple way to approximate the value of \(\pi\) using elementary calculus.
Buffon’s Needle Problem
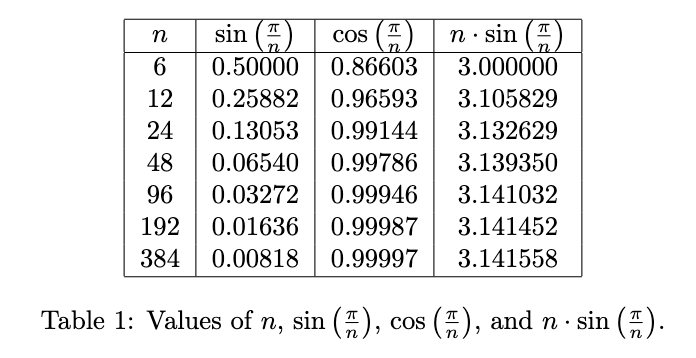
An interesting and intriguing experiment relating to the mysteries of \(\pi\) is Buffon’s needle problem. The good news is, you can try it at home yourself! Grab some needles or toothpicks and a sheet of paper. Draw a pair of parallel lines on the paper and make sure that the distance between them is equal to twice the length of the needle. Now begin randomly tossing needles at the paper. As you throw them, record the ratio between the number of needles thrown and the number of needles that touch one of the lines. Watch what happens to this ratio as the number of needles you throw increases. Notice anything?
Buffon’s needle problemDetermine the value of π using sticks, McZusatz, Wikipedia
The ratio will actually begin to converge towards \(\pi\).
In 1901, Mario Lazzarini, an Italian mathematician, was supposedly able to approximate \(\pi\) to 6 decimal places using Buffon’s needle problem. After tossing a needle 3408 times, he obtained the ratio \(\frac{355}{113} \approx 3.1415929\), the closest ratio to \(\pi\) among all ratios between two numbers of up to 5 digits. However, it is possible that Lazzarini repeated the experiment until he obtained the most desirable result. Nevertheless, Buffon’s needle problem allows for an interesting and seemingly random method of approximating \(\pi\) that gives us a refresher from converging infinite series and polygon approximations. So, how does it actually work?
The derived formula for Buffon’s needle problem is shown below.
\[ \pi = 2 \ast \frac{\text{length of toothpick}}{\text{distance between two lines}} \ast \frac{\text{total number of toothpicks tossed}}{\text{number of line-crossing toothpicks}} \]
By conveniently setting the distance between the lines to be twice the length of the toothpick, the ratio will be \(1/2\). That way, the 2 and \(\frac{1}{2}\) cancel each other out and we are left with \(\pi = \frac{\text{total number of toothpicks tossed}}{\text{number of line-crossing toothpicks}}\).
The proof for this formula is not simple and involves the use of integrals to determine the probability of a needle touching a line. We first introduce 2 variables, \(x\) and \(\theta\). \(x\) is the distance from the midpoint of a needle to the closest line and \(\theta\) is the acute angle between the needle and one of the parallel lines.
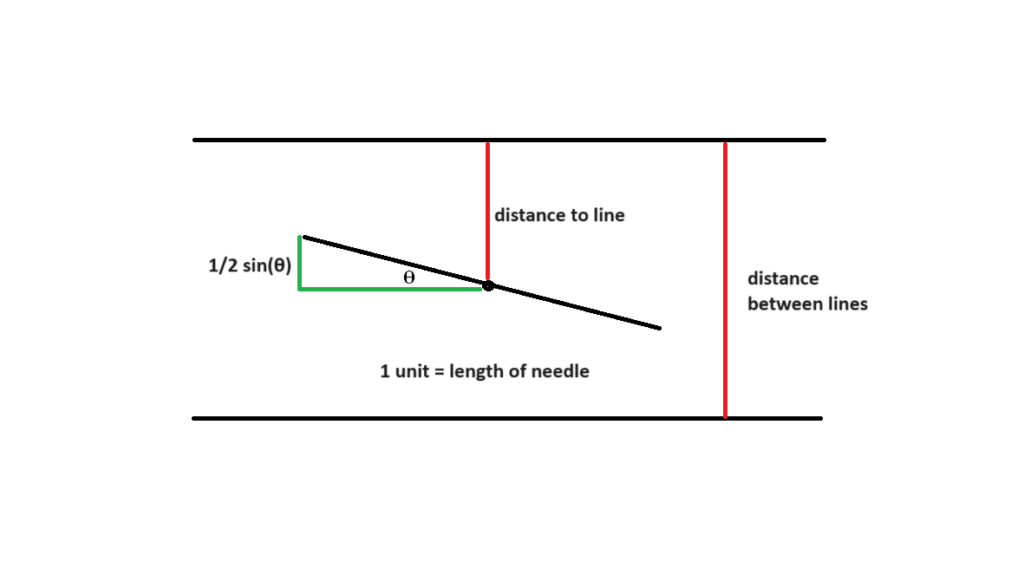
Buffon’s needle problem
There are 3 cases; (1) the needle is longer than the distance between the lines, (2) the needle is equal to the distance between the lines, (3) the needle is shorter than the distance between the lines.
First, let’s look at the 2nd case, which is the simplest. Based on the diagram, we can see that in order for a needle to touch one of the lines, \(D \le \frac{1}{2} \sin\theta\).
When graphing \(D\) along the \(y\)-axis and \(\frac{1}{2} \sin(\theta)\) along the \(x\)-axis, we obtain a curve. By calculating the area of the curve under \(D=\frac{1}{2}\) (representing \(D \le \frac{1}{2} \sin \theta\)), and dividing it by the total area of the rectangle, we can calculate the probability of a needle touching one of the lines.
The area under the curve is equal to the integral of
\[ \int_0^{\pi} \frac{1}{2} \sin \theta \,d\theta = 1 \]
The area of the rectangle is \(\frac{\pi}{2}\). Thus, the probability is
\[ \frac{1}{\frac{\pi}{2}} = \frac{2}{\pi} \]
The proof for a “short” needle is more complicated but can still be derived using elementary calculus.
Let \(P\) be the probability that a needle with length \(l\) dropped on a plane with two parallel lines \(t\) units apart touches a line when landing.
We can separate \(P\) into two probabilities \(P = P_1 \ast P_2\), where \(P_1\) is the probability that the center of the needle is close enough to the line so that the needle can potentially cross it, and \(P_2\) is the probability that the needle actually touches the line.
We can see that the needle can potentially cross the line only if the distance from the center to the line is less than \(\frac{l}{2}\), or \(D \le \frac{l}{2}\). That means that \(P_1 = \frac{\frac{l}{2} + \frac{l}{2}}{t} = \frac{l}{t}\). We add \(\frac{l}{2}\) twice because there is a left and right side of the needle and thus there are two possible regions, one on the left and one on the right where \(D \le \frac{l}{2}\).
For calculating \(P_2\), we assume that the center of the needle is within \(\frac{l}{2}\) of one of the lines. To make things easier, let’s say the length of a needle is 2 units and so the center must be within 1 unit of a parallel line. If the center of the needle is at \(x\), then it will only touch the line if it falls in the range of \(2\theta\) radians, which is shown in Figure 3 as the shaded portion.
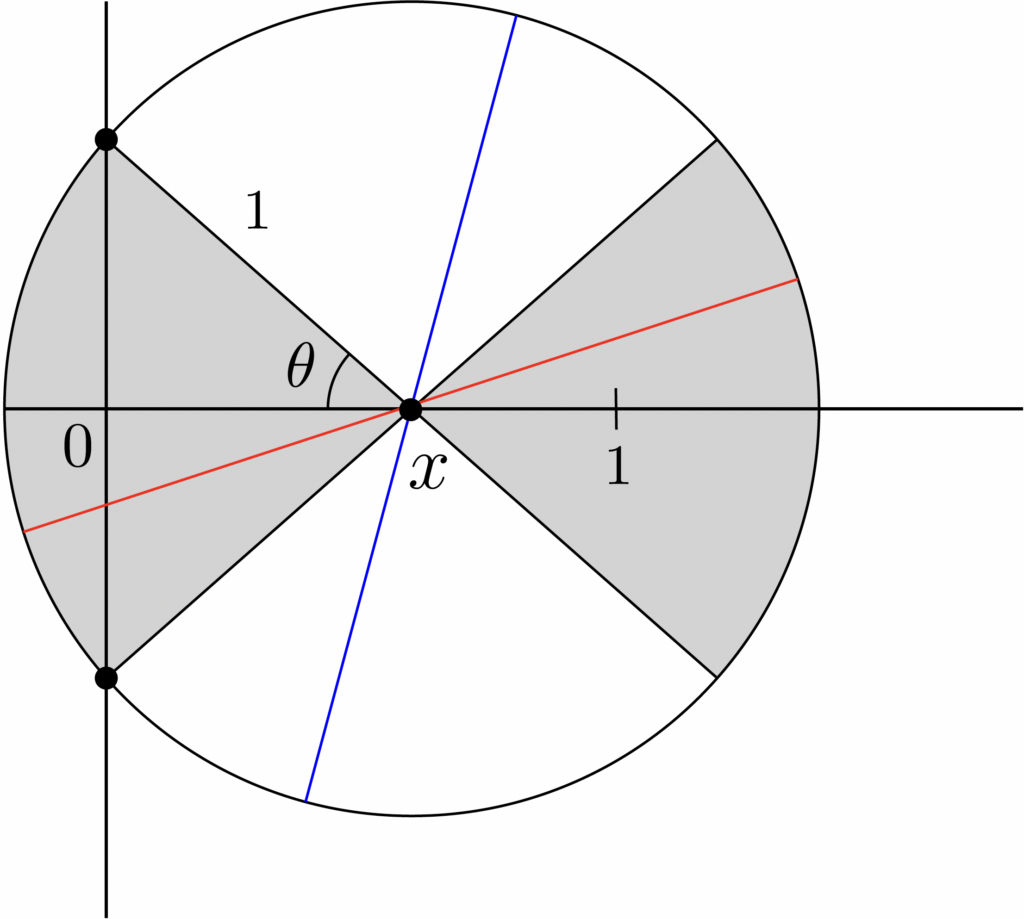
If a needle falls into the shaded portion, that means it touches a line.
We can see that \(\theta = \arccos(x)\) and so we can integrate
\[ 2 \frac{\arccos(x)}{\pi} \]
from 0 to 1 to determine the probability that the angle \(\theta\) falls within the shaded area.
\[ P_2 = \int_0^1 \frac{2\arccos(x)}{\pi} \,dx \\ = \frac{2}{\pi} \int_0^1 \cos^{-1}(x) \,dx \\ = \frac{2}{\pi} \cdot 1 = \frac{2}{\pi}. \]
Multiplying \(P_1\) and \(P_2\) we obtain
\[ P = \frac{2l}{t\pi}. \]
That is the proof of the formula for Buffon’s Needle problem.
Conclusion
The study of $\pi$ and the never-ending quest to discover more digits has captivated us throughout history. Through this article, we’ve explored the history of $\pi$ as well as some estimations that you can do yourself as well as the math behind them.
With the arrival of modern technology, calculating $\pi$ to as many digits as possible is no longer as useful. In reality, the search for $\pi$ has uses only as a benchmark for supercomputers. As computers have developed over the years, so have our methods for approximating $\pi$. However, beyond that is the same thirst for knowledge and understanding. The relationship of $\pi$ with the natural geometry of our world has remained a topic of interest and intrigue to all mathematicians and math enjoyers alike for ages, and it will certainly continue to be.
Sources
- https://www.bbc.com/future/article/20240313-pi-day-the-number-that-can-help-unravel-the-universe
- https://math.stackexchange.com/questions/2393503/finding-the-value-of-pi-using-calculus
- https://www.physicsforums.com/threads/derivation-of-pi-using-calculus.926116/
- http://www.ams.org/publicoutreach/feature-column/fcarc-pi-calc
- https://mathworld.wolfram.com/piFormulas.html
- https://www.britannica.com/science/pi-mathematics
- https://www3.trincoll.edu/employees/pbrown/MathModeling/StudentProjects/buffon/what.html
- https://en.wikipedia.org/wiki/Approximations_of_%CF%80
- https://en.wikipedia.org/wiki/pi
- https://www.storagereview.com/news/storagereview-lab-breaks-pi-calculation-world-record-with-over-202-trillion-digits
- https://mste.illinois.edu/activity/buffon/
- https://en.wikipedia.org/wiki/Buffon%27s_needle_problem
- https://commons.wikimedia.org/wiki/File:Streicholz-Pi.jpg
