Cosine of $\pi$ is $\boxed{-1}$.

1 Unit Circle

There are multiple ways to find $\cos \pi$. One option is to use the unit circle:

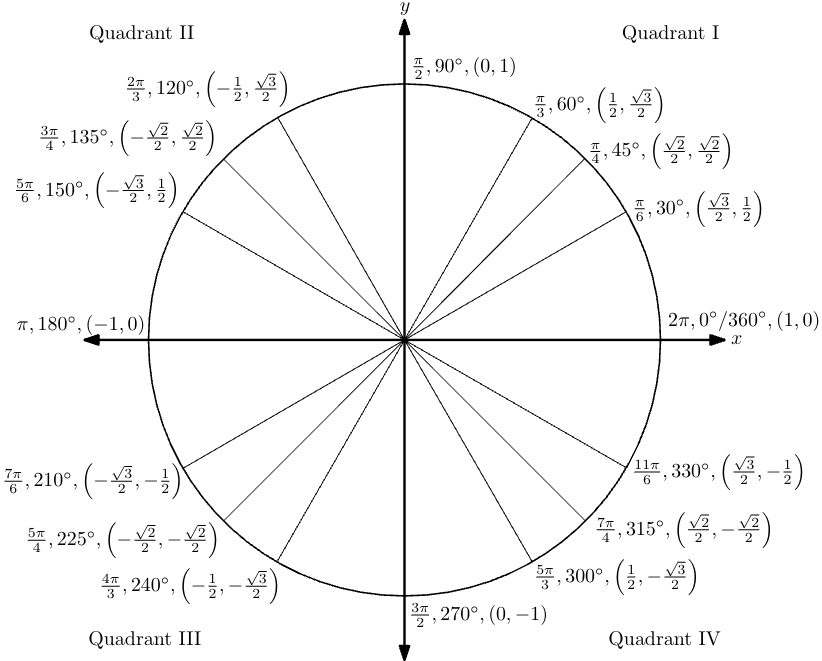
Notice that $\cos \pi = \cos 180^\circ$. Recall that $180^\circ$ is a straight angle, so the terminal side in standard position would intersect the unit circle on the $x$-axis at $(-1,0)$. The value of the $\cos $ is the $x$ coordinate on the unit circle. Thus
$$ \cos \pi = \cos180^\circ = \boxed{-1} $$

2 Graphing

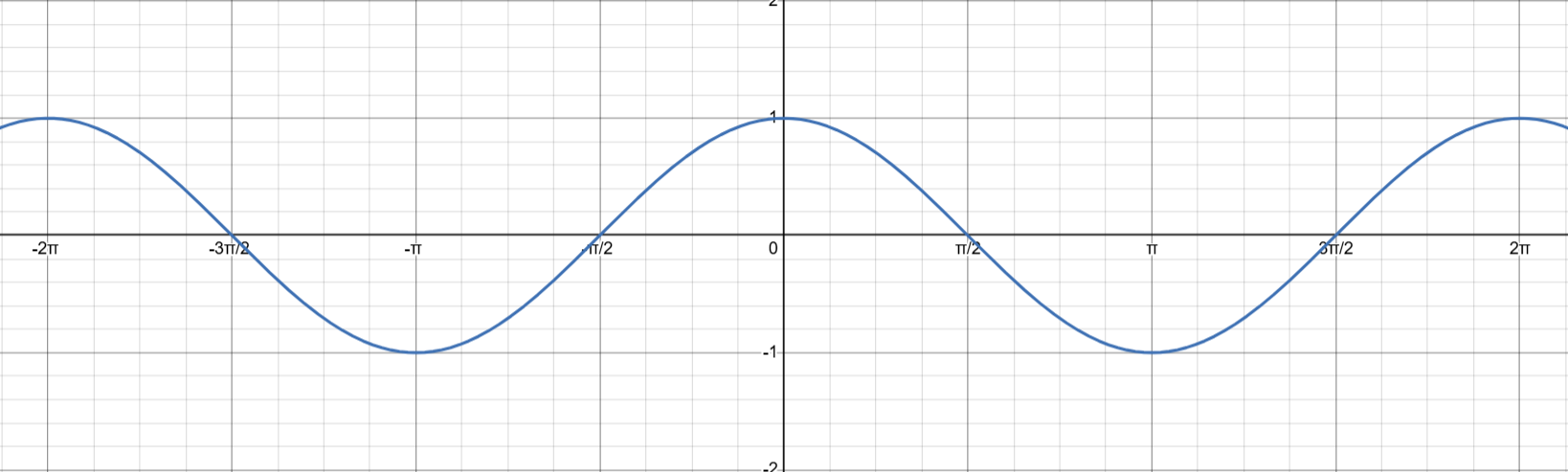
Alternatively, you might remember the graph of the cosine wave and that the period of $y = \cos x$ is $2\pi$. The period of $y = \cos x$ is $2\pi$ because $2\pi$ represents full rotation, so any two angles differing by $2\pi$ have the same terminal side. In fact, such angles have a special name – they are called co-terminal.
Since $\cos 0 = 1$ and $\pi$ is halfway between $0$ and $2\pi$, from the sketch it should be clear that

$$ \cos\pi = -1 $$