Master Calculus! Get instant help on “I Aced Calculus AP” App. Hundreds of flashcards and practice questions at your fingertips. Download now on the App Store and Google Play.

11 Oct 2024
The value of \(\cos 180^\circ\) is:
$\cos 180^\circ = \boxed{-1}$
To understand why, let’s look at the unit circle. The cosine of an angle corresponds to the \(x\)-coordinate of the point on the unit circle at that angle. We measure angles by moving counterclockwise from the positive \(x\)-axis. Thus at \(180^\circ\), we’re at the opposite side of the unit circle at the point with coordinates \((-1, 0)\).
Here, the \(x\)-coordinate is \(-1\), which is the value of \(\cos 180^\circ\).
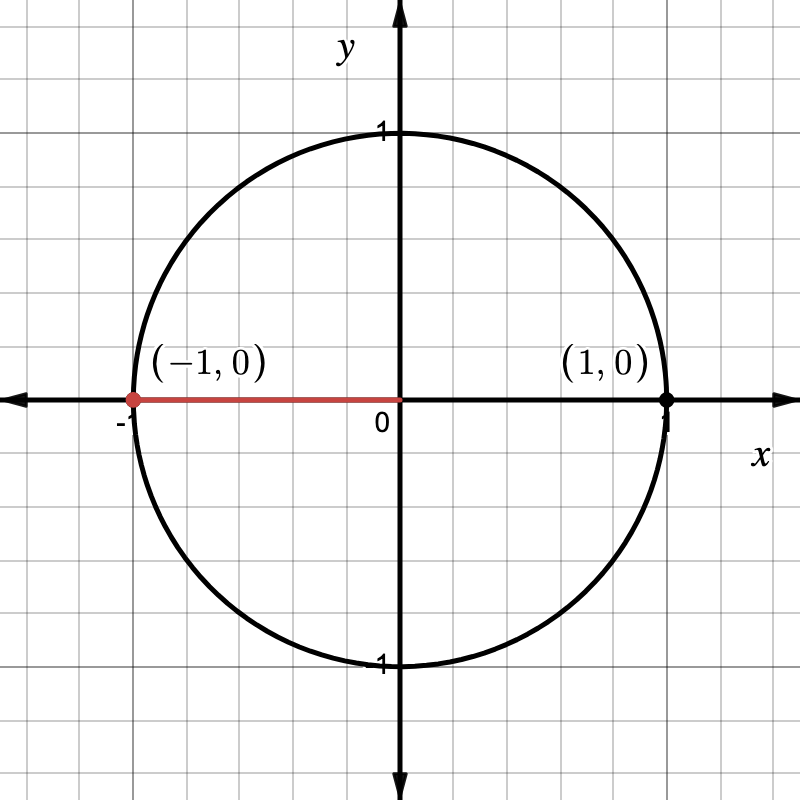
The unit circle helps visualize this because angles measured from \(0^\circ\) which is the direction of the positive \(x\)-axis (starting at \((1, 0)\) lead us along the circle to the \(180^\circ\), which is furthest point on the left side of the circle. The value of \(\cos\) of the given angle is the \(x\)-coordinate of the point on the unit circle. This is also why \(\cos\) of \(0^\circ\) is \(1\), and \(\cos\) of \(90^\circ\) is \(0\) – look at the \(x\)-coordinates of those points.
Therefore, \(\cos 180^\circ = \boxed{-1}\).