
April 2, 2025
🛌 Evidence-based strategies to improve sleep quality, latency, and depth Sleep is essential for top performance. Here we have outlined our top 15 sleep aid suggestions tested by our team members. While each individual strategy might not have a strong effect, the more strategies you implement, the stronger the cumulative effect. Circadian Rhythm Reset (Morning & […]
Read article
November 30, 2024
A mistakes journal is one of the most effective tools for mastering math, especially in complex subjects like Calculus or competitive problem-solving. Instead of just moving past errors, this tool helps you analyze them, identify patterns, and turn them into opportunities for growth. Done properly, a mistakes journal becomes your personal roadmap to improving accuracy […]
Read article
November 30, 2024
Math competitions are not just about solving math problems—they are rigorous mental exercises that build critical skills needed for lifelong success. Participants develop resilience, strategic thinking, creativity, and the discipline to face challenges head-on. Here’s how math competitions teach valuable life skills. 1. Resilience and Adaptability In math competitions, no one has all the answers […]
Read article
November 28, 2024
Did you get the AMC 10 results and are not happy with the score? Here are some questions for the parent and student to discuss as they plan for the comeback. The questions are grouped by topic to help guide a productive and constructive conversation: 1. Test-Day Performance How did you feel during the actual […]
Read article
November 24, 2024
As a high-achieving math student, you know that precision and creativity are key to acing tough exams. Achieving razor-sharp focus, especially under test pressure, can be challenging. Let’s discuss actionable steps and exercises that you can use to train unbreakable focus while maintaining the mental agility needed to solve complex problems. 1. Train Your Super […]
Read article
November 3, 2024
Below are key strategies to help you prepare in the final two days before your AMC 10 and 12 test, covering sleep, food, physical activity, math practice, and mindset. 1. Sleep: Essential for focus Two nights before: Aim for a full night of sleep (7-9 hours). Good rest two nights before the test has a […]
Read article
September 2, 2024
Calculus is one of the most powerful tools in mathematics, used for everything from physics to economics. But what is its origins? The development of calculus was a long process, shaped by many brilliant mathematicians over thousands of years. This article explores the key moments in the history of calculus, from ancient methods to the […]
Read article
August 27, 2024
Introduction Everyone knows \(\pi\). The ratio between the circumference and diameter of a circle is often approximated as 3.14. For many, it’s the first irrational number they encounter—a number so renowned that it even has its own day of celebration. But how was \(\pi\) actually discovered? The history of \(\pi\) stretches over thousands of years, […]
Read article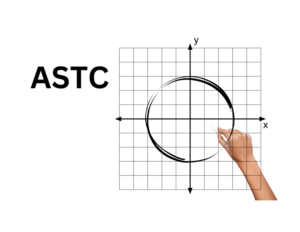
August 25, 2024
Have you ever had trouble remembering when sines, cosines, and tangents are positive or negative? If so, you may want to remember the mnemonic ASTC, which stands for All, Sine, Tangent, Cosine and can be remembered as “All Students Take Calculus.” The acronym tells you which trig functions are positive in each quadrant, starting from […]
Read article